线段树合并学习笔记

First Post:

Last Update:

Word Count:
6.4k

Read Time:
33 min

今天模拟赛考到了线段树合并，发现不是很熟悉，所以今天恶补一下。

写起来才发现：这东西这么好写啊？

只有题，没有讲解，想看讲解可以看别的博客。

upd：我的代码里都是先把东西插到对应的线段树里，然后再 开始合并。但如果边合并边插入，是可以写垃圾回收省空间的。代码懒得改了。

题单

[Vani有约会] 雨天的尾巴 /【模板】线段树合并

模板，但感觉比一些其他题难一点。

首先考虑暴力。

我们可以对每个点维护一个桶，然后暴力链加。

因为最后要求每个点的最大值，所以维护桶好像不太行，可以换成维护 set 或者权值线段树。

但暴力链加肯定是不行的，所以考虑树上差分，最后只需要做一遍类似前缀和的合并即可。

如果你用权值线段树，那么这个合并就是线段树合并，复杂度 。

如果你用 set 或其他平衡树，那么这个合并就是启发式合并，复杂度 。

这里说一点，需要线段树合并的题空间复杂度一般都为 ，因为动态开点线段树。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
#include"bits/stdc++.h"
#define re register
#define int long long
#define ls(p) tr[p].ls
#define rs(p) tr[p].rs
using namespace std;
const int maxn=1e5+10,V=1e5;
int n,m,cnt,segcnt;
int head[maxn],rt[maxn],ans[maxn];
struct edge{
    int to,nxt;
}e[maxn<<1];
struct node{
    int fa,siz,dep,hson,top;
}t[maxn];
struct node1{
    int sum,id;
    inline node1 operator + (const node1 &a)const{
        if(sum>a.sum) return {sum,id};
        else if(sum==a.sum) return {sum,min(id,a.id)};
        else return a;
    }
};
struct tree{
    int ls,rs;
    node1 s;
}tr[maxn*50];
inline void add(int u,int v){
    e[++cnt]={v,head[u]};
    head[u]=cnt;
}
inline void dfs1(int u,int fa){
    t[u].fa=fa,t[u].siz=1,t[u].dep=t[fa].dep+1;
    for(re int i=head[u];i;i=e[i].nxt){
        int v=e[i].to;
        if(v==fa) continue;
        dfs1(v,u);
        t[u].siz+=t[v].siz;
        if(!t[u].hson||t[v].siz>t[t[u].hson].siz) t[u].hson=v;
    }
}
inline void dfs2(int u,int top){
    t[u].top=top;
    if(!t[u].hson) return;
    dfs2(t[u].hson,top);
    for(re int i=head[u];i;i=e[i].nxt){
        int v=e[i].to;
        if(v==t[u].fa||v==t[u].hson) continue;
        dfs2(v,v);
    }
}
inline int lca(int u,int v){
    while(t[u].top!=t[v].top){
        if(t[t[u].top].dep<t[t[v].top].dep) swap(u,v);
        u=t[t[u].top].fa;
    }
    return t[u].dep<t[v].dep?u:v;
}
inline void up(int p){tr[p].s=tr[ls(p)].s+tr[rs(p)].s;}
inline void add(int p,int pos,int val){tr[p].s.sum+=val,tr[p].s.id=pos;}
inline void update(int l,int r,int pos,int val,int &p){
    if(!p) p=++segcnt;
    if(l==r){add(p,pos,val);return;}
    int mid=(l+r)>>1;
    if(pos<=mid) update(l,mid,pos,val,ls(p));
    else update(mid+1,r,pos,val,rs(p));
    up(p);
}
inline int merge(int l,int r,int p,int p1){
    if(!p||!p1) return p+p1;
    if(l==r){
        add(p,l,tr[p1].s.sum);
        return p;
    }
    int mid=(l+r)>>1;
    ls(p)=merge(l,mid,ls(p),tr[p1].ls);
    rs(p)=merge(mid+1,r,rs(p),tr[p1].rs);
    up(p);
    return p;
}
inline void dfs(int u,int fa){
    for(re int i=head[u];i;i=e[i].nxt){
        int v=e[i].to;
        if(v==fa) continue;
        dfs(v,u);
        rt[u]=merge(1,V,rt[u],rt[v]);
    }
    ans[u]=tr[rt[u]].s.id;
}
signed main(){
#ifndef ONLINE_JUDGE
    freopen("1.in","r",stdin);
    freopen("1.out","w",stdout);
#endif
    ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
    cin>>n>>m;
    for(re int i=1,u,v;i<n;++i) cin>>u>>v,add(u,v),add(v,u);
    dfs1(1,0),dfs2(1,1);
    for(re int i=1,u,v,z,Lca;i<=m;++i){
        cin>>u>>v>>z;Lca=lca(u,v);
        update(1,V,z,1,rt[u]);update(1,V,z,1,rt[v]);
        update(1,V,z,-1,rt[Lca]);update(1,V,z,-1,rt[t[Lca].fa]);
    }
    dfs(1,0);
    for(re int i=1;i<=n;++i) cout<<ans[i]<<'\n';
    return 0;
}

[USACO17JAN] Promotion Counting P

子树逆序对数量，这东西本质上就是个二维数点。

而且这题啥也没卡，所以写啥都能过。

不过因为在练习线段树合并，所以我写了线段树合并。

对于这种求每个点的子树信息的问题，经常可以每个点维护一颗线段树，然后从叶子向上合并，最后查询。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
#include"bits/stdc++.h"
#define re register
#define int long long
#define ls(p) tr[p].ls
#define rs(p) tr[p].rs
using namespace std;
const int maxn=1e5+10,V=1e9;
int n,segcnt,cnt;
int a[maxn],head[maxn],rt[maxn],ans[maxn];
struct edge{
    int to,nxt;
}e[maxn];
struct tree{
    int ls,rs;
    int sum;
}tr[maxn*50];
inline void add(int u,int v){
    e[++cnt]={v,head[u]};
    head[u]=cnt;
}
inline void up(int p){tr[p].sum=tr[ls(p)].sum+tr[rs(p)].sum;}
inline void add_val(int p,int val){tr[p].sum+=val;}
inline void update(int l,int r,int pos,int val,int &p){
    if(!p) p=++segcnt;
    if(l==r){add_val(p,val);return;}
    int mid=(l+r)>>1;
    if(pos<=mid) update(l,mid,pos,val,ls(p));
    else update(mid+1,r,pos,val,rs(p));
    up(p);
}
inline int merge(int l,int r,int p,int p1){
    if(!p||!p1) return p+p1;
    if(l==r){add_val(p,tr[p1].sum);return p;}
    int mid=(l+r)>>1;
    ls(p)=merge(l,mid,ls(p),tr[p1].ls);
    rs(p)=merge(mid+1,r,rs(p),tr[p1].rs);
    up(p);
    return p;
}
inline int query(int l,int r,int L,int R,int p){
    if(!p) return 0;
    if(l>=L&&r<=R) return tr[p].sum;
    int mid=(l+r)>>1,res=0;
    if(L<=mid) res+=query(l,mid,L,R,ls(p));
    if(R>mid) res+=query(mid+1,r,L,R,rs(p));
    return res;
}
inline void dfs(int u){
    for(re int i=head[u];i;i=e[i].nxt){
        int v=e[i].to;
        dfs(v);
        rt[u]=merge(1,V,rt[u],rt[v]);
    }
    ans[u]=query(1,V,a[u]+1,V,rt[u]);
}
signed main(){
#ifndef ONLINE_JUDGE
    freopen("1.in","r",stdin);
    freopen("1.out","w",stdout);
#endif
    ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
    cin>>n;
    for(re int i=1;i<=n;++i) cin>>a[i],update(1,V,a[i],1,rt[i]);
    for(re int i=2,fa;i<=n;++i) cin>>fa,add(fa,i);
    dfs(1);
    for(re int i=1;i<=n;++i) cout<<ans[i]<<'\n';
    return 0;
}

Lomsat gelral

第一次做这道题还是在学 DSU on tree 的时候。

依旧可以线段树合并，维护的信息比较简单，略过了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
#include"bits/stdc++.h"
#define re register
#define int long long
#define ls(p) tr[p].ls
#define rs(p) tr[p].rs
using namespace std;
const int maxn=1e5+10;
int n,cnt,segcnt;
int head[maxn],ans[maxn],rt[maxn];
struct edge{
    int to,nxt;
}e[maxn<<1];
struct node{
    int sum,ans;
    inline node operator + (const node &a)const{
        if(sum>a.sum) return {sum,ans};
        else if(sum==a.sum) return {sum,ans+a.ans};
        else return a;
    }
};
struct tree{
    int ls,rs;
    node s;
}tr[maxn<<5];
inline void add(int u,int v){
    e[++cnt]={v,head[u]};
    head[u]=cnt;
}
inline void up(int p){tr[p].s=tr[ls(p)].s+tr[rs(p)].s;}
inline void add(int p,int pos,int val){tr[p].s.sum+=val,tr[p].s.ans=pos;}
inline void update(int l,int r,int pos,int val,int &p){
    if(!p) p=++segcnt;
    if(l==r){add(p,pos,val);return;}
    int mid=(l+r)>>1;
    if(pos<=mid) update(l,mid,pos,val,ls(p));
    else update(mid+1,r,pos,val,rs(p));
    up(p);
}
inline int merge(int l,int r,int p,int p1){
    if(!p||!p1) return p+p1;
    if(l==r){add(p,l,tr[p1].s.sum);return p;}
    int mid=(l+r)>>1;
    ls(p)=merge(l,mid,ls(p),tr[p1].ls);
    rs(p)=merge(mid+1,r,rs(p),tr[p1].rs);
    up(p);
    return p;
}
inline void dfs(int u,int fa){
    for(re int i=head[u];i;i=e[i].nxt){
        int v=e[i].to;
        if(v==fa) continue;
        dfs(v,u);
        rt[u]=merge(1,n,rt[u],rt[v]);
    }
    ans[u]=tr[rt[u]].s.ans;
}
signed main(){
#ifndef ONLINE_JUDGE
    freopen("1.in","r",stdin);
    freopen("1.out","w",stdout);
#endif
    ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
    cin>>n;
    for(re int i=1,x;i<=n;++i) cin>>x,update(1,n,x,1,rt[i]);
    for(re int i=1,u,v;i<n;++i) cin>>u>>v,add(u,v),add(v,u);
    dfs(1,0);
    for(re int i=1;i<=n;++i) cout<<ans[i]<<' ';
    return 0;
}

[POI2011] ROT-Tree Rotations

前面三道基本都是模板，这道要动脑子了。

upd：在做完以后感觉这是为数不多需要动脑子的题。

考虑先序遍历是怎么输出的：根-左子树-右子树。

所以逆序对是由这些部分贡献的：左子树内部，右子树内部，左子树和右子树。

然后考虑交换左右子树带来的影响是什么。

可以发现，只有第三部分被影响了。

每个点维护一颗权值线段树，在左儿子和右儿子的线段树合并时，可以轻松得到逆序对数量。

这里借用题解一张图。

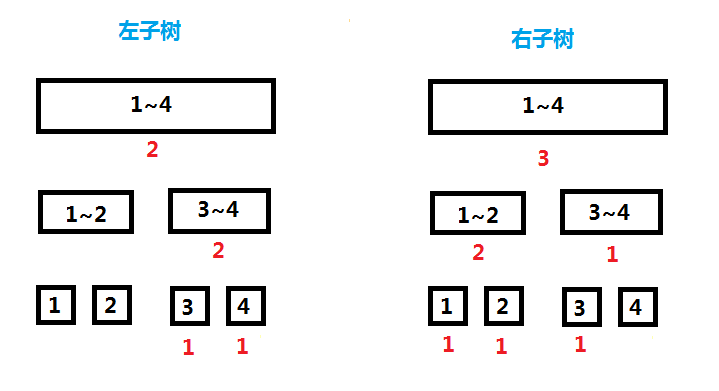
5cd96945b450241844.png (719×391)

可以发现，如果不交换，那么逆序对数量就是当前节点左儿子的右半区间的权值乘上右儿子左半区间的权值；如果交换就反过来。

这个东西可以在线段树合并时算出来，然后取个 即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
#include"bits/stdc++.h"
#define re register
// #define int long long
#define ls(p) tr[p].ls
#define rs(p) tr[p].rs
using namespace std;
const int maxn=2e5+10;
int n,segcnt;
long long ans,ans1,ans2;
struct tree{
    int ls,rs,sum;
}tr[maxn<<5];
inline void up(int p){tr[p].sum=tr[ls(p)].sum+tr[rs(p)].sum;}
inline void add(int p,int val){tr[p].sum+=val;}
inline void update(int l,int r,int pos,int val,int &p){
    if(!p) p=++segcnt;
    if(l==r){add(p,val);return;}
    int mid=(l+r)>>1;
    if(pos<=mid) update(l,mid,pos,val,ls(p));
    else update(mid+1,r,pos,val,rs(p));
    up(p);
}
inline int merge(int l,int r,int p,int p1){
    if(!p||!p1) return p+p1;
    if(l==r){add(p,tr[p1].sum);return p;}
    ans1+=1ll*tr[rs(p)].sum*tr[tr[p1].ls].sum;
    ans2+=1ll*tr[ls(p)].sum*tr[tr[p1].rs].sum;
    int mid=(l+r)>>1;
    ls(p)=merge(l,mid,ls(p),tr[p1].ls);
    rs(p)=merge(mid+1,r,rs(p),tr[p1].rs);
    up(p);
    return p;
}
inline int dfs(){
    //pos为当前节点的线段树的根
    int pos=0,val;cin>>val;
    if(!val){
        int ls=dfs(),rs=dfs();
        ans1=ans2=0;
        pos=merge(1,n,ls,rs);
        ans+=min(ans1,ans2);
    }
    else update(1,n,val,1,pos);
    return pos;
}
signed main(){
#ifndef ONLINE_JUDGE
    freopen("1.in","r",stdin);
    freopen("1.out","w",stdout);
#endif
    ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
    cin>>n;
    dfs();
    cout<<ans;
    return 0;
}

Blood Cousins

双倍经验：[Cnoi2019] 雪松果树

这题用线段树合并？感觉不如我 bfs 序+dfs 序啊。

具体做法可以看 东方Project相关试题选做，在第 49 道。

线段树合并做法也很简单。

把询问都挂到询问点 的 级祖先上，然后每个点维护一颗以深度为下标的权值线段树，把子树信息都合并上来以后回答所有询问即可。

我没写。

[湖南集训] 更为厉害

这题用线段树合并？感觉不如我二维数点啊。

把 的位置分讨一下：如果是 的祖先答案能直接算，如果在 子树内就是二维数点。

事实上线段树合并也是在干二维数点这件事。

也可以这么说：线段树合并可以在线的完成子树数点。

我写的二维数点，所以不放代码了。

Dominant Indices

每个点维护一颗以深度为下标的权值线段树，节点上维护最大值即可。

因为维护的是深度，所以答案记得要减一下。

Tree Requests

用 [Cnoi2019] 雪松果树 那道题的套路可以把问题转化为 美好的每一天 的弱化版。

线段树合并做法：每个点维护一颗以深度为下标的权值线段树，节点上维护一个状压后的值，修改是单点异或，合并就正常合并。

Blood Cousins Return

题意： 级儿子颜色数。

用 [Cnoi2019] 雪松果树 那道题的套路可以把问题转化为区间颜色数。

这东西有一万种做法，可以参考 [SDOI2009] HH的项链。

线段树合并做法：每个点维护一颗以深度为下标的权值线段树，节点上维护一个 set，合并时启发式合并即可，复杂度 。

Tree and Queries

把子树看成区间后可以把问题转化为 Marisa采蘑菇 的弱化版。

用线段树合并做这题很麻烦，完全不如 DSU on tree 或莫队简单，但还是说一下。

每个点维护一颗以颜色为下标的权值线段树，然后你就会发现：出现次数怎么搞？

没想到，有兴趣的看 题解 吧。

Escape Through Leaf

设 表示从点 出发到叶子的最小代价，转移为

这是个斜率优化的形式，所以可以用李超树优化。

然后要从子树转移来，李超树合并即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
#include"bits/stdc++.h"
#define re register
#define int long long
using namespace std;
const int maxn=1e5+10,maxv=2e5+10,inf=1e18;
int n,cnt,segcnt;
int head[maxn],a[maxn],b[maxn],f[maxn],rt[maxn];
struct edge{
    int to,nxt;
}e[maxn<<1];
struct line{
    int k,b;
}lin[maxn];
struct tree{
    int ls,rs,id;
}tr[maxn<<1];
inline void add(int u,int v){
    e[++cnt]={v,head[u]};
    head[u]=cnt;
}
inline int calc(int x,int id){return lin[id].k*(x-maxn)+lin[id].b;}
inline void update(int l,int r,int id,int &p){
    if(!p){p=++segcnt;tr[p].id=id;return;}
    int mid=(l+r)>>1;
    if(calc(mid,id)<calc(mid,tr[p].id)) swap(id,tr[p].id);
    if(calc(l,id)<calc(l,tr[p].id)) update(l,mid,id,tr[p].ls);
    if(calc(r,id)<calc(r,tr[p].id)) update(mid+1,r,id,tr[p].rs);
}
inline int query(int l,int r,int pos,int p){
    if(!p) return inf;
    int mid=(l+r)>>1,res=calc(pos,tr[p].id);
    if(l==r) return res;
    if(pos<=mid) return min(res,query(l,mid,pos,tr[p].ls));
    else return min(res,query(mid+1,r,pos,tr[p].rs));
}
inline int merge(int l,int r,int a,int b){
    if(!a||!b) return a+b;
    if(l==r){
        if(calc(l,tr[b].id)<calc(l,tr[a].id)) swap(tr[a].id,tr[b].id);
        return a;
    }
    int mid=(l+r)>>1;
    tr[a].ls=merge(l,mid,tr[a].ls,tr[b].ls);
    tr[a].rs=merge(mid+1,r,tr[a].rs,tr[b].rs);
    update(l,r,tr[b].id,a);
    return a;
}
inline void dfs(int u,int fa){
    for(re int i=head[u];i;i=e[i].nxt){
        int v=e[i].to;
        if(v==fa) continue;
        dfs(v,u);
        rt[u]=merge(1,maxv,rt[u],rt[v]);
    }
    f[u]=query(1,maxv,a[u]+maxn,rt[u]);
    if(f[u]==inf) f[u]=0;
    lin[u]={b[u],f[u]};
    update(1,maxv,u,rt[u]);
}
signed main(){
#ifndef ONLINE_JUDGE
    freopen("1.in","r",stdin);
    freopen("1.out","w",stdout);
#endif
    ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
    cin>>n;
    for(re int i=1;i<=n;++i) cin>>a[i];
    for(re int i=1;i<=n;++i) cin>>b[i];
    for(re int i=1,u,v;i<n;++i) cin>>u>>v,add(u,v),add(v,u);
    dfs(1,0);
    for(re int i=1;i<=n;++i) cout<<f[i]<<" ";
    return 0;
}

[HNOI2012] 永无乡

考虑给每个连通块开一颗线段树，查询直接线段树上二分。

因为有合并，所以线段树合并即可，需要用并查集维护连通性。

代码很久以前写的，比较丑，不放了。

有人想做加强版吗：[Ynoi2014] 等这场战争结束之后。

题解可以看 操作树学习笔记，在最后一道。

[PKUWC2018] Minimax

线段树合并优化 DP。

现在这种题都只能紫了，前两天 [NOI2020] 命运 也降了，这东西真有这么普及吗？

设 表示点 的权值为 的概率。

若点 为叶子或只有一个儿子的情况都是简单的，我们考虑有两个儿子的情况。

假设现在要转移权值 ，那么这个权值要么没在子树内出现过，要么在左/右子树内。

没出现过概率肯定都是 ，不用管。下面假设其在左子树内，右子树同理。

首先分讨一下点 是取最小值还是最大值。

若取到最大值，那么 要想取到 ，就必须让右儿子的权值小于 。

若取到最小值，那么 要想取到 ，就必须让右儿子的权值大于 。

因为左儿子取到权值 也是有概率的，也要算上。

综上，转移为

右子树同理，转移为

观察到，转移需要维护一个前缀和以及一个后缀和。

所以我们现在需要一个东西，支持：快速合并两个数组，快速维护前缀和以及后缀和。

所以想到了线段树合并。

具体实现就是把后面括号里的一堆东西当成乘法标记打到节点上。

在合并时，如果两边都有节点，就继续往下走并累加标记：走左儿子就加后缀和，走右儿子就加前缀和。

如果走到有一侧没有节点了，就把标记打上去。

比普通的合并要难写，不过也还行。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
#include"bits/stdc++.h"
#define re register
#define int long long
#define ls(p) tr[p].ls
#define rs(p) tr[p].rs
using namespace std;
const int maxn=3e5+10,mod=998244353,inv=796898467;
int n,m,segcnt,ans;
int fa[maxn],ch[maxn][2];
int a[maxn],b[maxn];
int rt[maxn];
struct tree{
    int ls,rs;
    int sum,tag;
}tr[maxn<<5];
inline void up(int p){tr[p].sum=(tr[ls(p)].sum+tr[rs(p)].sum)%mod;}
inline void add(int p,int val){tr[p].sum+=val;}
inline void mul(int p,int val){if(!p) return;tr[p].sum=tr[p].sum*val%mod,tr[p].tag=tr[p].tag*val%mod;}
inline void down(int p){if(tr[p].tag!=1) mul(ls(p),tr[p].tag),mul(rs(p),tr[p].tag),tr[p].tag=1;}
inline void update(int l,int r,int pos,int val,int &p){
    if(!p) p=++segcnt,tr[p].tag=1;
    if(l==r){add(p,val);return;}
    int mid=(l+r)>>1;down(p);
    if(pos<=mid) update(l,mid,pos,val,ls(p));
    else update(mid+1,r,pos,val,rs(p));
    up(p);
}
inline int merge(int l,int r,int mul1,int mul2,int P,int p,int p1){
    //mul1 给左子树打的标记（转移 1）
    //mul2 给右子树打的标记（转移 2）
    if(!p&&!p1) return 0;
    if(!p){mul(p1,mul2);return p1;}
    if(!p1){mul(p,mul1);return p;}
    int mid=(l+r)>>1;down(p),down(p1);
    int sl=tr[ls(p)].sum,sr=tr[rs(p)].sum,sl1=tr[tr[p1].ls].sum,sr1=tr[tr[p1].rs].sum;
    //注意这里必须先把值都存下来，因为直接传 tr[ls(p)].sum,tr[rs(p)].sum 的话，ls(p) 和 rs(p) 会因为已经被改了而出错
    ls(p)=merge(l,mid,(mul1+(1-P+mod)*sr1%mod)%mod,(mul2+(1-P+mod)*sr%mod)%mod,P,ls(p),tr[p1].ls);
    rs(p)=merge(mid+1,r,(mul1+P*sl1%mod)%mod,(mul2+P*sl%mod)%mod,P,rs(p),tr[p1].rs);
    up(p);
    return p;
}
inline void dfs(int u){
    if(!ch[u][0]) update(1,m,a[u],1,rt[u]);
    if(ch[u][0]&&!ch[u][1]) dfs(ch[u][0]),rt[u]=rt[ch[u][0]];
    if(ch[u][0]&&ch[u][1]) dfs(ch[u][0]),dfs(ch[u][1]),rt[u]=merge(1,m,0,0,a[u],rt[ch[u][0]],rt[ch[u][1]]);
}
inline void dfs1(int l,int r,int p){
    if(l==r){ans=(ans+l*b[l]%mod*tr[p].sum%mod*tr[p].sum%mod)%mod;return;}
    int mid=(l+r)>>1;down(p);
    dfs1(l,mid,ls(p)),dfs1(mid+1,r,rs(p));
}
signed main(){
#ifndef ONLINE_JUDGE
    freopen("1.in","r",stdin);
    freopen("1.out","w",stdout);
#endif
    ios::sync_with_stdio(0),cin.tie(0),cout.tie(0); 
    cin>>n;
    for(re int i=1;i<=n;++i) cin>>fa[i];
    for(re int i=1;i<=n;++i) cin>>a[i];
    for(re int i=1;i<=n;++i){
        if(!fa[i]) continue;
        if(!ch[fa[i]][0]) ch[fa[i]][0]=i;
        else ch[fa[i]][1]=i;
    }
    for(re int i=1;i<=n;++i){
        if(ch[i][0]) a[i]=a[i]*inv%mod;
        else b[++m]=a[i];
    }
    sort(b+1,b+m+1);
    for(re int i=1;i<=n;++i) if(!ch[i][0]) a[i]=lower_bound(b+1,b+m+1,a[i])-b;
    dfs(1),dfs1(1,m,rt[1]);
    cout<<ans;
    return 0;
}

[NOI2022] 众数

百 万 deque 过 大 江。

如果只有一个序列，那么很好做，维护一颗权值线段树即可。

但现在有多个序列，我们考虑如何找出绝对众数。

绝对众数有一个很经典的做法：摩尔投票法。

例题：yyy loves Maths VI (mode)

主要想法就是：每次拿两个数，如果不一样就都删掉，否则不删。

如果最后删空了，说明没有绝对众数；否则剩下的这个数可能为绝对众数（所以还需要检验）。

然后对于这道题，我们只需要把那些有绝对众数的序列拿出来做摩尔投票，然后检验最后得到的结果即可。

可能会有疑问：为什么不用考虑不是绝对众数的部分？

因为不是任何一个序列绝对众数的数一定不会成为答案。

这比较显然，因为这个数在任何一个序列里的出现次数都严格小于一半，那么它在总序列里的出现次数也一定严格小于一半。

所以我们可以先对每个有绝对众数的序列内部做摩尔投票，然后把每个序列合并起来，最终得到答案。

实现上，可以对每个序列用一颗权值线段树维护出现次数，用 deque/链表/平衡树 维护真实序列。

合并时线段树直接合并，deque/平衡树 需要启发式合并。

不过，在赛场上，许多选手都因为 deque 爆了。

所以用 STL 时一定要注意空间！

为了致敬，我写了 deque 启发式合并。

注意合并时要按顺序！

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
#include"bits/stdc++.h"
#define re register
#define int long long
#define ls(p) tr[p].ls
#define rs(p) tr[p].rs
using namespace std;
const int maxn=5e5+10,maxm=1e6+10;
int n,m,q,segcnt;
int rt[maxn],tmp[maxn],rev[maxm];	
struct node{
    int siz;
    deque<int> q;
}t[maxn];
struct node1{
    int sum,id;
    inline node1 operator + (const node1 &a)const{
        if(sum>a.sum) return {sum,id};
        else return a;	
    }
};
struct tree{
    int ls,rs;
    node1 s;
}tr[maxn<<5];
int top;
int stk[maxn<<5];
inline int newnode(){return top?stk[top--]:++segcnt;}
inline void erase(int p){ls(p)=rs(p)=0,tr[p].s={0,-1};stk[++top]=p;}
inline void up(int p){tr[p].s=tr[ls(p)].s+tr[rs(p)].s;}
inline void add(int p,int pos,int val){tr[p].s.id=pos,tr[p].s.sum+=val;}
inline void update(int l,int r,int pos,int val,int &p){
    if(!p) p=newnode();
    if(l==r){add(p,pos,val);return;}
    int mid=(l+r)>>1;
    if(pos<=mid) update(l,mid,pos,val,ls(p));
    else update(mid+1,r,pos,val,rs(p));
    up(p);
}
inline int query(int l,int r,int pos,int p){
    if(!p) return 0;
    if(l==r) return tr[p].s.sum;
    int mid=(l+r)>>1;
    if(pos<=mid) return query(l,mid,pos,ls(p));
    else return query(mid+1,r,pos,rs(p));
}
inline int merge(int l,int r,int p,int p1){
    if(!p||!p1) return p+p1;
    if(l==r){add(p,l,tr[p1].s.sum);return p;}
    int mid=(l+r)>>1;
    ls(p)=merge(l,mid,ls(p),tr[p1].ls);
    rs(p)=merge(mid+1,r,rs(p),tr[p1].rs);
    up(p);erase(p1);
    return p;
}
inline void solve1(int x,int y){
    update(0,m,y,1,rt[x]);
    ++t[x].siz;
    t[x].q.push_back(y);
}
inline void solve2(int x){
    update(0,m,t[x].q.back(),-1,rt[x]);
    --t[x].siz;
    t[x].q.pop_back();
}
inline void solve3(int k){
    node1 ans={0,-1};
    for(re int i=1;i<=k;++i) cin>>tmp[i],tmp[i]=rev[tmp[i]];
    for(re int i=1,res;i<=k;++i){
        if(t[tmp[i]].siz/2>=tr[rt[tmp[i]]].s.sum) continue;
        res=tr[rt[tmp[i]]].s.sum-(t[tmp[i]].siz-tr[rt[tmp[i]]].s.sum);
        if(tr[rt[tmp[i]]].s.id==ans.id) ans.sum+=res;
        else{
            if(ans.sum<res) ans={res-ans.sum,tr[rt[tmp[i]]].s.id};
            else if(ans.sum==res) ans={0,-1};
            else ans.sum-=res;
        }
    }
    if(!(~ans.id)) cout<<-1<<'\n';
    else{
        int tot=0,res=0;
        for(re int i=1;i<=k;++i) tot+=t[tmp[i]].siz,res+=query(0,m,ans.id,rt[tmp[i]]);
        if(res>tot/2) cout<<ans.id<<'\n';
        else cout<<-1<<'\n';
    }
}
inline void solve4(int x,int y,int z){
    if(t[x].siz<t[y].siz){
        rev[z]=y;
        rt[y]=merge(0,m,rt[x],rt[y]);
        t[y].siz+=t[x].siz;t[x].siz=0;
        while(!t[x].q.empty()) t[y].q.push_front(t[x].q.back()),t[x].q.pop_back();
    } 
    else{
        rev[z]=x;
        rt[x]=merge(0,m,rt[x],rt[y]);
        t[x].siz+=t[y].siz;t[y].siz=0;
        while(!t[y].q.empty()) t[x].q.push_back(t[y].q.front()),t[y].q.pop_front();
    }
}
signed main(){
#ifndef ONLINE_JUDGE
    freopen("1.in","r",stdin);
    freopen("1.out","w",stdout);
#endif
    ios::sync_with_stdio(0),cin.tie(0),cout.tie(0); 
    cin>>n>>q;m=n+q;
    for(re int i=1;i<=n;++i){
        cin>>t[i].siz;rev[i]=i;
        for(re int j=1,x;j<=t[i].siz;++j){
            cin>>x;
            t[i].q.push_back(x);
            update(0,m,x,1,rt[i]);
        }
    }
    for(re int i=1,op,x,y,z,k;i<=q;++i){
        cin>>op;
        if(op==1) cin>>x>>y,solve1(rev[x],y);
        if(op==2) cin>>x,solve2(rev[x]);
        if(op==3) cin>>k,solve3(k); 
        if(op==4) cin>>x>>y>>z,solve4(rev[x],rev[y],z);
    }
    return 0;	
}
≡