Slope Trick学习笔记
Last Update:
Word Count:
Read Time:
引入
太困难了···
Slope Trick 是一种维护凸包的方法,通常用来优化 dp。
一般可以使用 Slope Trick 优化的 dp 方程需要满足:
- 是连续的
- 是分段一次函数
- 有凸性
一些性质:
- 两个凸函数相加还是凸函数
- 凸函数加一次函数还是凸函数
一些名词:
- 拐点:函数斜率改变的点
- 决策点:纵坐标为答案的点

具体内容通过例题讲解,不然还是太难懂了。
例题
Sequence *2200
首先考虑暴力 dp。
因为要将序列变为非降数列,所以有一个性质:最终序列的数集不会变大。
证明很好证:
因为只有序列某一位置严格递减时,我们才会进行修改。
而修改要么将前面的数减到和后面的数一样大,要么将后面的数加到和前面的数一样大。
这两个操作都不会让数集变大。
所以设 表示将第 个数变为 的最小代价,转移为
这是 的,虽然能通过本题,但我们考虑优化。
我们把这个 dp 变一下,方便理解。
设 表示将第 个数变为 的最小代价, 表示将第 个数变为 的最小代价。
则转移为
我们固定 ,以 为横坐标,dp 值为纵坐标建系。
这里偷同学几张图。
可以得到, 为:
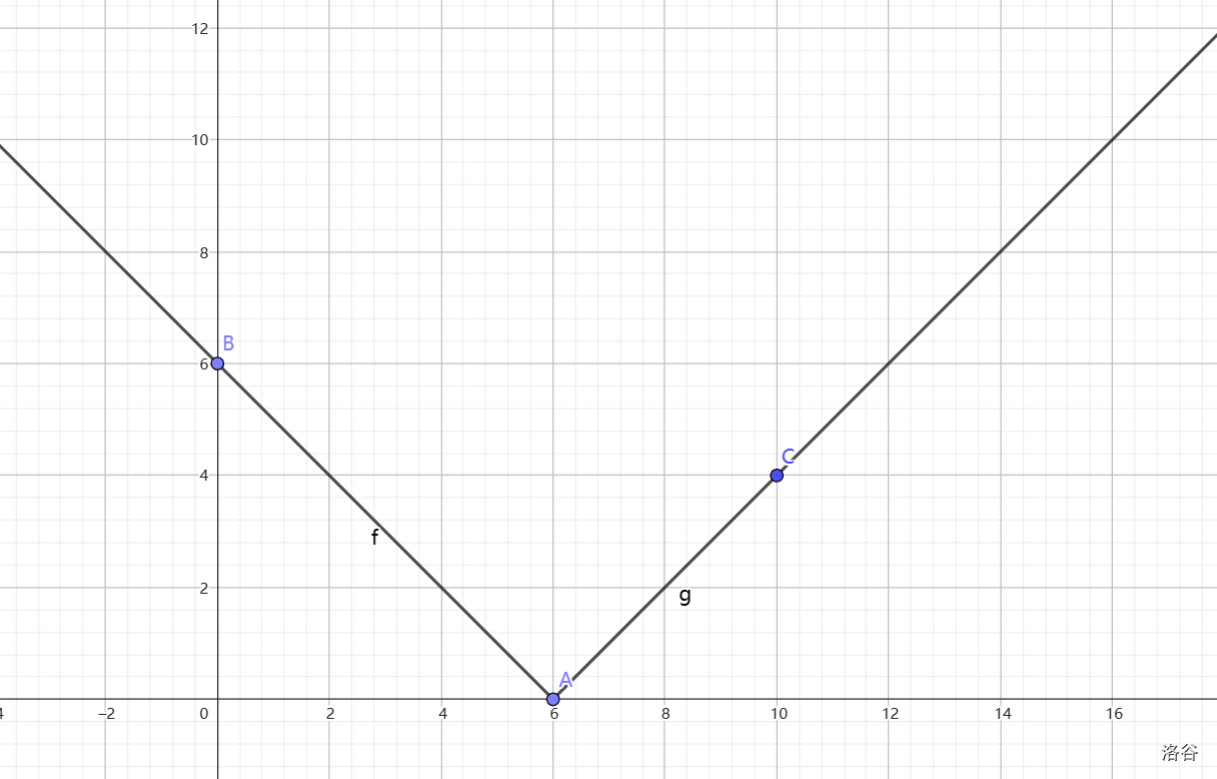
因为 是 的前缀 ,所以 为:
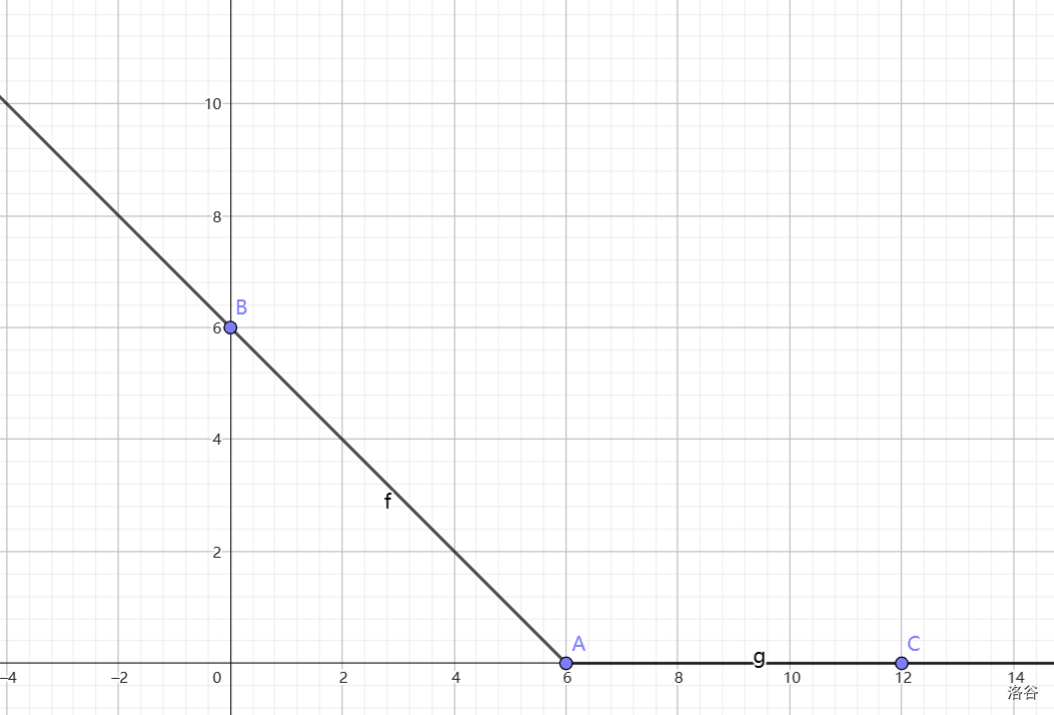
根据 dp 式可以发现, 是由 这个函数加一个绝对值函数得到的。
这里需要分类讨论:绝对值函数的拐点在 的决策点的左/右侧。
如果在右侧,那么是这样的
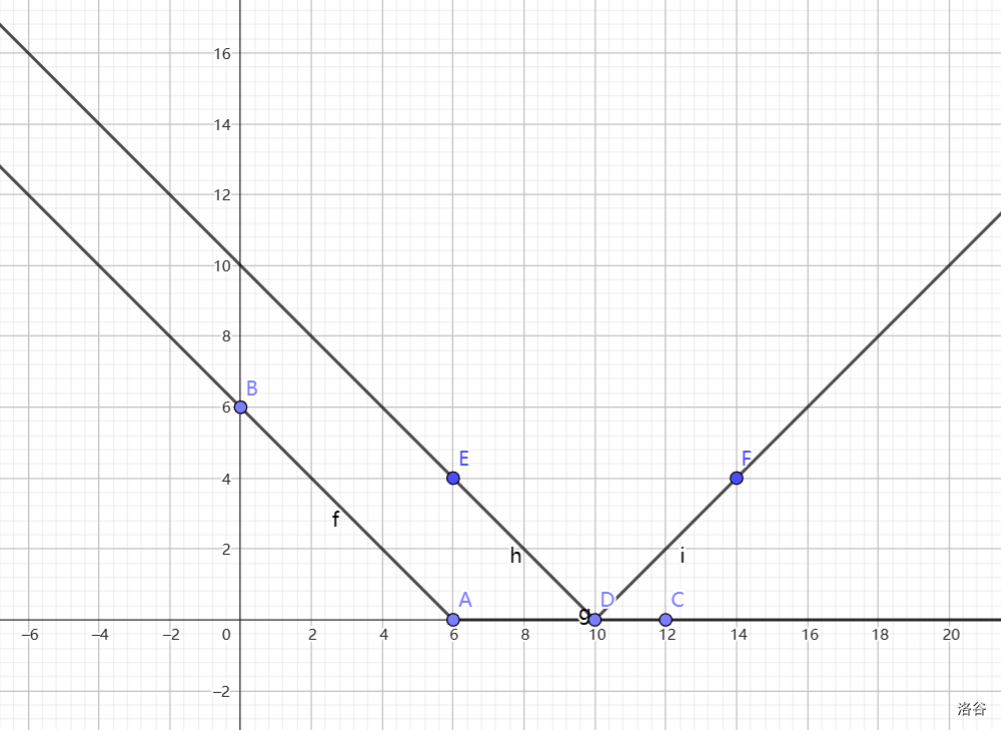
相加后可以得到 为
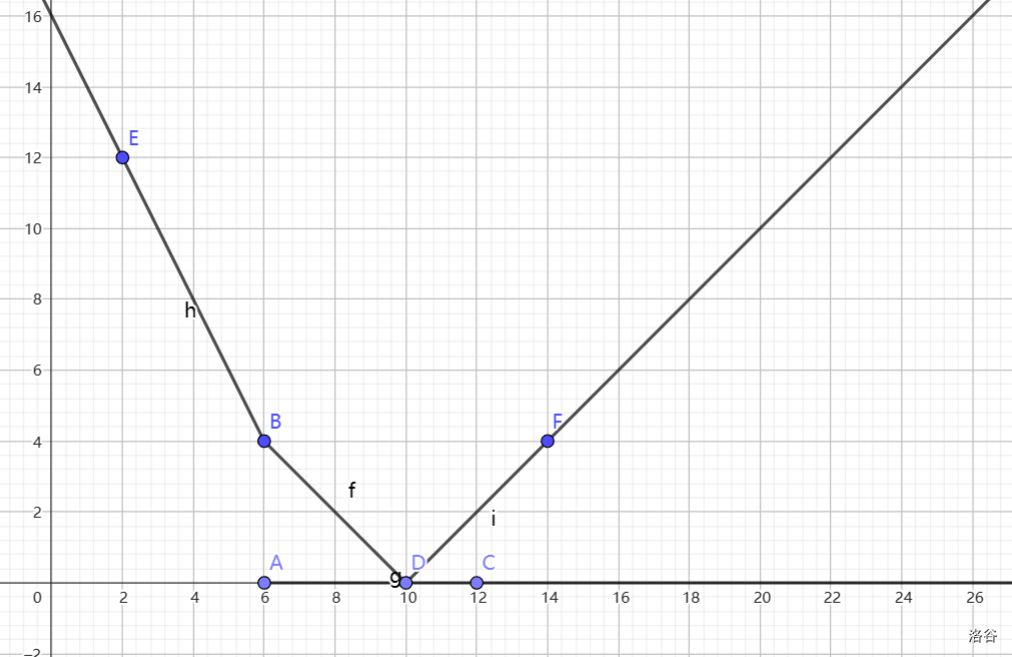
从而可以得到 为
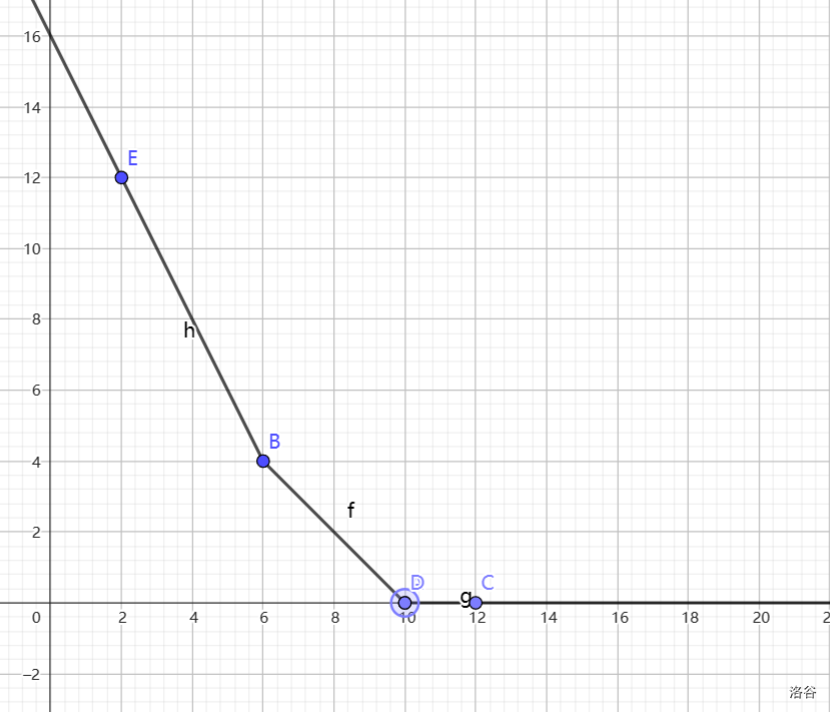
如果在左侧,那么是这样的
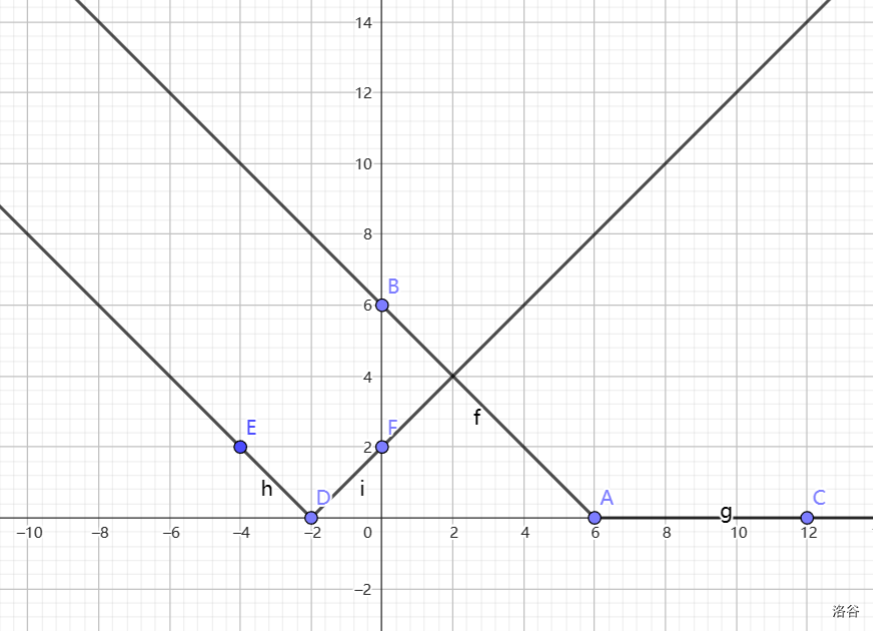
相加后可以得到 为
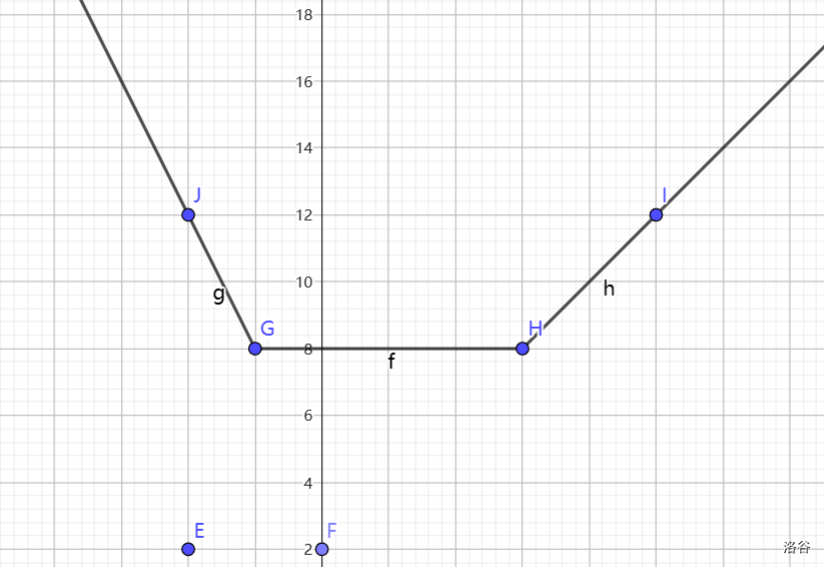
从而可以得到 为
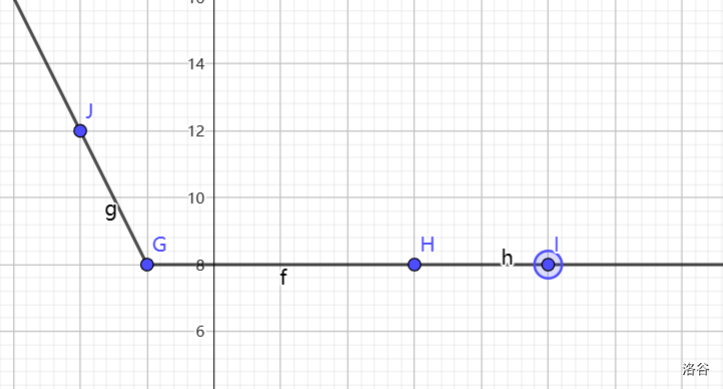
答案为 的最小值。
可以发现,只有绝对值函数的拐点在决策点左侧时,答案才会更新。
那么答案变化了多少呢?
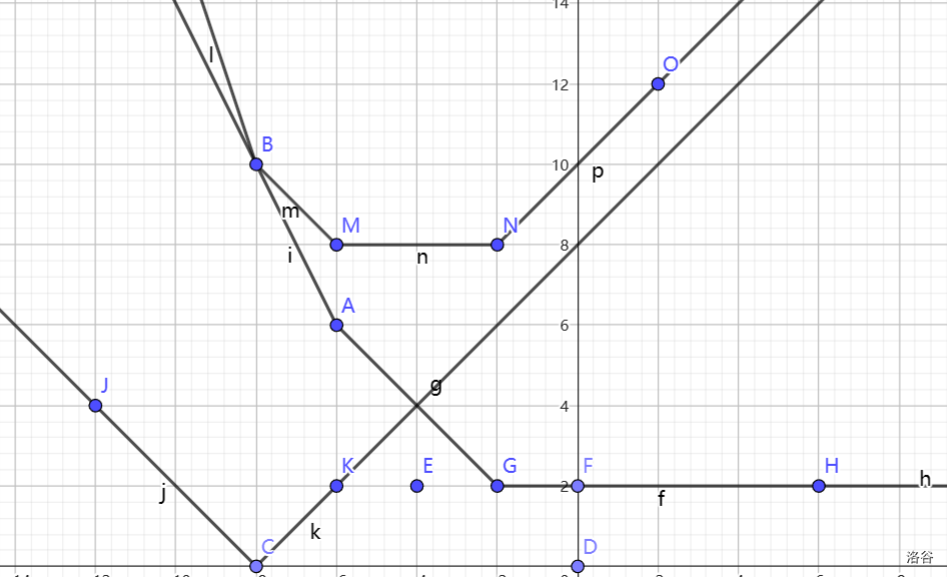
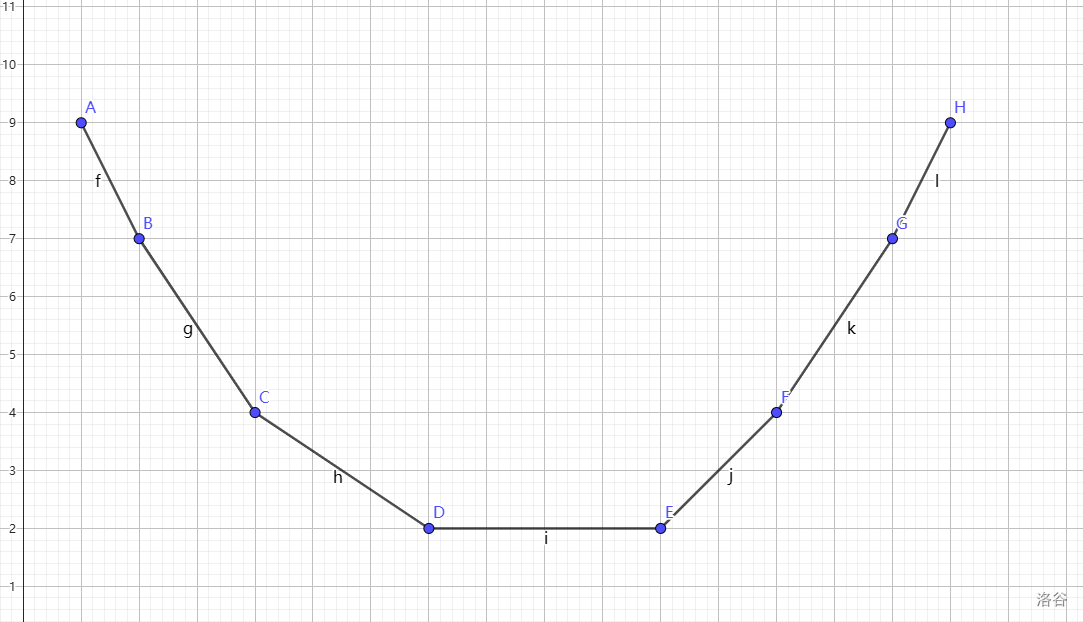
图中 BAGH 为原来的 ,JCK 为加的绝对值函数,BMNO 为加完以后的 。
那么答案的变化量为 N 和 G 的纵坐标之差。
通过观察几何性质,可以发现这东西就等于原绝对值函数拐点的横坐标。
然后考虑怎么维护函数 。(接下来我可能会说的比较抽象且啰嗦,因为我实在不知道怎么才能说明白)
我们可以维护一个堆,堆里存函数的所有拐点。这道题中我们需要维护大根堆,这样堆顶就是我们需要的决策点。
然后我们把斜率挂到点上维护,当然我们需要钦定每个点维护的是左侧的线段还是右侧的线段。
这里我们钦定每个点维护左侧的线段的斜率。
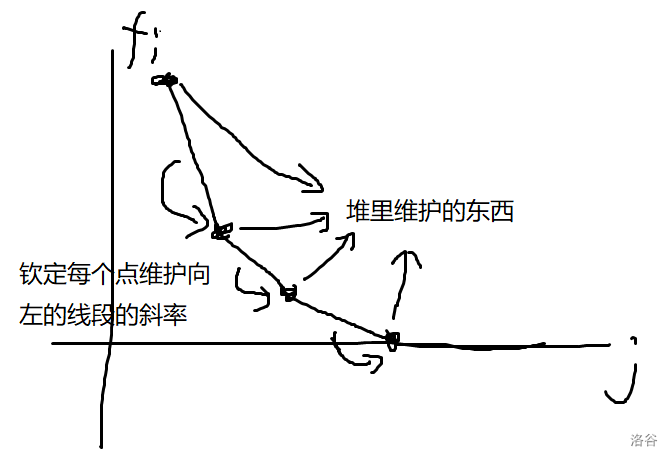
那这个斜率到底怎么表示呢?别急,看下面。
然后考虑加绝对值函数的操作。可以发现,这个操作事实上就是在让绝对值函数拐点左侧的函数斜率 -1,拐点右侧的函数斜率 +1。
当拐点在决策点右侧或决策点上时,我们会让拐点左侧的函数斜率 -1,右侧的函数斜率 +1。但因为取 了,所以右侧函数斜率还是 0。
对应到操作上,就是把绝对值函数拐点加进堆里。
可以发现,此时堆中每个点维护的对应线段的斜率就是其在堆中排名 -1 的相反数(因为这个函数的斜率都是负数)。
如果如果相邻两个点间的斜率差 怎么办?
那就把一个点插入多次。
但这样会存在一些假点,这些点并没有意义。
所以我们的斜率要变一下:堆中每个点维护的对应线段的斜率就是与其值相同的最左侧的点在堆中排名 -1 的相反数。
当拐点在决策点左侧时,因为要让拐点左侧的函数斜率 -1,右侧的函数斜率 +1,所以对应到操作上应该插入两个拐点,因为斜率变化为 2。
插入完后,我们还要把原来的决策点扔掉,因为它已经不是当前的决策点了。
然后我们维护完了这个函数,且求出了答案。
复杂度
1 | |
Buy Low Sell High *2400
首先考虑暴力 dp。
设 表示第 天有 股的最大值,转移为
答案为 。
感性理解一下,可以发现这个函数是凸的。
但这个函数的变化就不是每次加一个凸函数了,而是函数平移然后取 。
第一个转移可以直接转移过来,这样后面的取 都是和原函数取 了。
后面的两个转移可以看成把函数加一个平移向量 和 。
先考虑左上平移:
图中 A1B1C1D1 为平移后的函数。
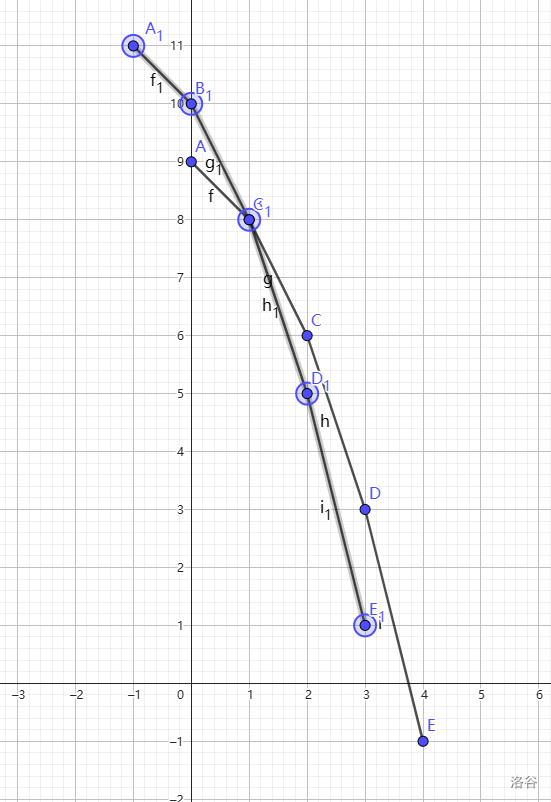
取完 后长这样
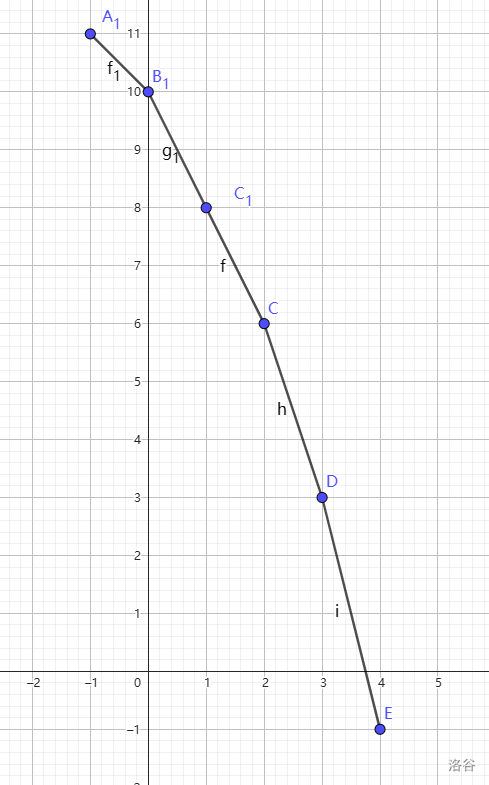
对于左上平移,可以发现,原函数中斜率 移动斜率的的部分都会被平移后的函数在取 时覆盖掉,而 移动斜率的的部分不会被影响。
也就是说斜率 移动斜率的的部分排名集体左移,其他部分不变。
然后中间会产生一条新线段,斜率为 。
当然,图中的 A 点应该被删掉,因为我们的答案是和 y 轴的交点,所以 y 轴左侧的点都不能保留。
注意:这个操作只有在原函数中存在斜率 移动斜率时才有意义,否则不会有任何影响。
然后考虑右下平移:
事实上是完全一样的。
因为你只需要把 A1B1C1D1 视为原函数,ABCD 视为平移后的函数即可。
综上,我们依旧考虑用一个堆来维护这个函数,堆里存函数的所有斜率(不是拐点)。
我们维护大根堆,这样方便判断左上平移是否需要操作。
而且删 A 点时只要把斜率最大的那个删了就行,因为函数的斜率单调递减。
那么怎么算答案呢?
这里还用上道题中的计算变化量的方法就不好用了。
但可以发现,这个函数的最小值是可以轻松得到的,就是 。
而且可以发现,因为相邻两个拐点的横坐标差为 -1,所以纵坐标之差就是斜率乘上 -1。
那么我们只需要用最小值加上所有纵坐标之差,就可以得到与 y 轴交点的纵坐标,也就是答案。
复杂度
1 | |
[ARC070E] NarrowRectangles
首先考虑暴力 dp。
不敢设状态的我设计了这样的 dp:
设 表示第 个向左/右移动 个单位长度的代价。
但这个东西没有前途,所以要换状态。
设 表示第 个长方形,左端点在 时的代价,转移为
这里的 ,不然带着个 +1 有点麻烦。
如果 是前缀 ,那么这道题和第一道题一模一样。
但这东西是对一个区间取 ,这就不好做了。
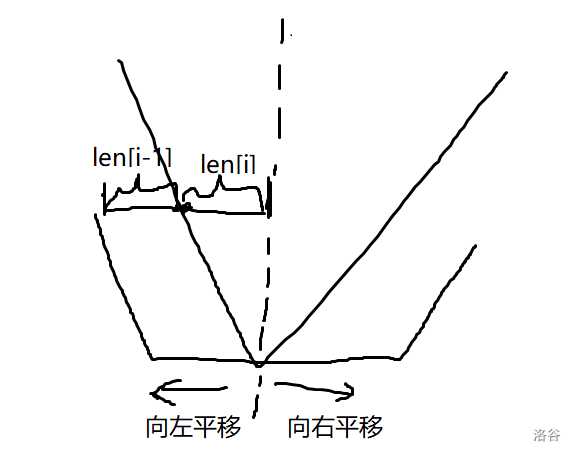
所以我们的 会是一个这样状物
然后我们分类讨论。
1.绝对值函数拐点在 D 左侧
答案变化量依旧为拐点横坐标之差。
我们把绝对值函数加上去以后,还要对每个点进行区间取 。
通过画图可以发现,我们依旧会把函数平移。
具体的,在 D 左侧的会向左平移,在 E 右侧的会向右平移。
所以我们可以维护两个堆,一个维护左侧点,一个维护右侧点。
加绝对值函数对左侧点的影响:这个部分和第一题一模一样,插两个扔一个。
但对右侧点可能也会有影响,因为 D 点在加完以后会成为右侧点,所以得把 D 扔到维护右侧点的堆里。
2.绝对值函数拐点在 E 右侧
基本同上,就是左右翻一下。
3.绝对值函数拐点在中间
那就左边插一个,右边插一个,分别表示斜率变化 1。
但有个很严重的问题没有解决:函数的平移怎么维护?
我们可以通过打标记来维护。
我们维护的标记记录函数真实移动的距离,堆里存的拐点事实上都是相对初始位置没有移动的。
所以在把一个点拿出来时,需要算上标记,得到它的真正位置。
把点放到堆里时,需要去除标记,得到相对初始位置没有移动的位置,然后放进去。
可以通过代码感受一下这个标记
1 | |
beautiful
对于这种括号匹配类问题,一般设右括号,这样比较好保证合法性。
设 表示前 个选了 个右括号,转移为
因为要保证合法,所以要保证 。
答案为 。
感性理解,这东西是下凸的,考虑 Slope Trick。
这两个转移可以看成原函数向上平移得到的新函数与函数向右上平移得到的新函数取 。
这不太好做,但我们可以转化一下。
我们先让函数向上平移,然后再进行第二个转移,即向右上平移。
但之前是向右上平移 ,现在是 。
这样就变成和原函数取 了,和第二道题的处理方式一模一样。
向上平移是有贡献的,要加上贡献。
但还得处理 的限制。
事实上,我们只需要类似第二题中扔掉 A 点一样,把那些不合法的点扔掉即可。
1 | |
参考文章: