字符串学到现在只会 SA,绷不住了。
还是得学学哈希,不然真考字符串就寄了。
什么是字符串哈希
通过一个函数把一个字符串映射为一个整数,这个函数就是哈希函数。
如何计算
我们通常采用多项式哈希。
设 为底数, 为模数,则
底数通常选择一个质数,模数通常选择一个大质数。
推荐:底数 131,模数 1926081719491001071
upd:131也被卡了,可以换成19260817。
如果要用的话记得开 int128,不然你一乘就炸了。
比较好记,就是江泽民主席的诞辰和建国时间拼起来再拼上071。
如果没想起来用 1e9+7 也行,不过容易被卡。
自然溢出还是算了吧,真怕被卡。
如何计算子串哈希值
首先处理出来前缀哈希值。
设第 位哈希值为 ,则
则 的哈希值,为
如何判断是否是回文串
正着算一遍哈希值,反着算一遍哈希值,如果一样说明是回文串。
如何得到两个串接起来得到的新串的哈希值
设两个字符串分别为 ,若把 接到 后面,则新串哈希值为
如果题目涉及到以上问题(即需要相乘)且你使用了大模数,请先想想会不会炸,需不需要 int128。
应用
大概就字符串匹配吧?还有别的用途吗?
字符串哈希厉害之处就在于可以在预处理后 匹配。
哈希还有一个常用搭配:二分。
因为字符串的匹配是有单调性的,长的匹配说明短的也匹配,所以可以二分长度然后用哈希判断。
例题
第一道题肯定要放模板啦。
求出每个字符串的哈希值,那么问题就变成了序列中有几个不同的数。
非常简单吧。
因为要求恰好一位不同,所以考虑枚举哪一位不同。
因为要把枚举到的那一位删掉,所以得处理所有串的前缀哈希,然后删这一位就是把前后的拼起来。
求子串哈希和怎么拼起来都在上文提到过。
然后就变成模板了。
复杂度
首先枚举 ,然后枚举每一段。
听上去很暴力对不对?但复杂度其实是有保证的。
总时间复杂度应该是 。
把 提出来,剩下的是个调和级数。
所以时间复杂度 。
用哈希匹配是 的,所以总复杂度 。
但有个需要注意的:这道题的串正着和反着视为相同,所以既要处理前缀哈希还要处理后缀哈希,只有都不相同时才能记录到答案。
首先,设 为答案,则 为答案的充要条件为 。
其次,答案一定是区间长度的约数。
所以我们从小到大枚举约数,然后哈希 判断。
复杂度
虽然约数个数是一个比 小一点的数,但依旧会 T。
考虑优化一下这个东西。
如果一个循环节出现了 2 次,另一个出现了 3 次,那么一定有一个会出现 6 次。
所以我们对每个质因数分别做,最后把它们合起来。
质因数个数是 级别的,可以通过。
因为通配符不超过 10,所以考虑把原串分成若干段,然后分段匹配,每段第一位为通配符。
设 表示分出来的第 个串能否匹配上查询串的 第 位。
转移为
这里的 代表按位或。
能否转移用哈希判断一下即可。
设通配符个数为 ,复杂度为
这不就是把上面那两个东西拼一块了吗。
设两个字符串分别为 ,那么这对字符串合法的条件为 。
移项,得到
对每个字符串求出这个东西,然后随便统计一下即可。
允许 次失配的字符串匹配。
考虑二分+哈希。
首先枚举所有可能匹配的子串,然后二分找到第一个失配的位置,把这个位置及之前的东西删掉,然后再进行这个过程。
如果失配次数 ,说明合法。
设原串长度为 ,模式串长度为 ,复杂度
Ciallo~(∠・ω< )⌒★
洛谷题解传送门
一道很好玩的题。
直接做可能没什么想法,那我们先对 和 讨论一下。
这里的 都是以原串为下标的。
1. 和 无交
那说明删除没任何影响。我们先找出所有匹配位置,然后随便算一下方案数就行了。
2. 和 有交。
不难发现,合法的 和 一定形如下图
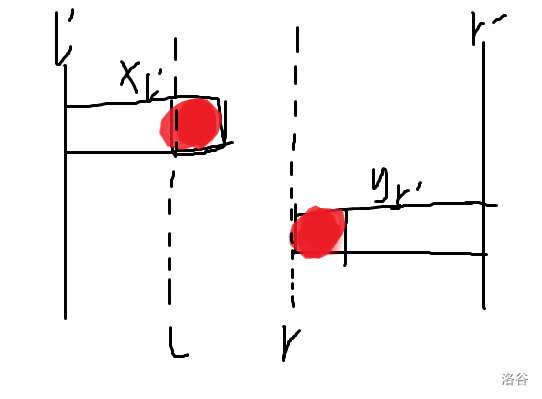
图中的 分别代表 。
设 长为 , 长为 。
红色部分为重复部分,长为 。
不难发现,对于这种情况,合法的方案数为 。
然后观察这种情况需要满足什么条件,不难发现,需要满足
不能等于 是因为这部分贡献已经在前面算过了,不能重复计算。
然后这东西就是个二维数点,数就完了。
数点时记得减去贡献。
树状数组 add 时可能会用到 0,整体加偏移量即可。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
| #include"bits/stdc++.h"
#define re register
#define int long long
#define lb(x) (x&(-x))
using namespace std;
const int maxn=4e5+10,base=131,mod=1e9+7;
int n,m,ans;
char s1[maxn],s2[maxn];
int pw[maxn];
int h1[maxn],h2[maxn];
int x[maxn],y[maxn];
struct BIT{
int tr[maxn];
inline void add(int x,int val){++x;while(x<maxn) tr[x]+=val,x+=lb(x);}
inline int query(int x){++x;int res=0;while(x>0) res+=tr[x],x-=lb(x);return res;}
}a,b;
inline int calc1(int l,int r){return ((h1[r]-h1[l-1]*pw[r-l+1]%mod)%mod+mod)%mod;}
inline int calc2(int l,int r){return ((h2[r]-h2[l-1]*pw[r-l+1]%mod)%mod+mod)%mod;}
inline bool check1(int pos,int len){
if(pos+len-1>n) return 0;
return calc1(pos,pos+len-1)==calc2(1,len);
}
inline bool check2(int pos,int len){
if(pos-len+1<1) return 0;
return calc1(pos-len+1,pos)==calc2(m-len+1,m);
}
inline void init(){
pw[0]=1;
for(re int i=1;i<maxn;++i) pw[i]=pw[i-1]*base%mod;
for(re int i=1;i<=n;++i) h1[i]=(h1[i-1]*base+s1[i])%mod;
for(re int i=1;i<=m;++i) h2[i]=(h2[i-1]*base+s2[i])%mod;
for(re int i=1,l,r,mid,res;i<=n;++i){
l=0,r=m,res=0;
while(l<=r){
mid=(l+r)>>1;
if(check1(i,mid)) res=mid,l=mid+1;
else r=mid-1;
}
x[i]=res;
l=0,r=m,res=0;
while(l<=r){
mid=(l+r)>>1;
if(check2(i,mid)) res=mid,l=mid+1;
else r=mid-1;
}
y[i]=res;
}
}
signed main(){
#ifndef ONLINE_JUDGE
freopen("1.in","r",stdin);
freopen("1.out","w",stdout);
#endif
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
cin>>(s1+1)>>(s2+1);n=strlen(s1+1),m=strlen(s2+1);
init();
for(re int i=1;i<=n;++i) if(y[i]==m) ans+=((i-m)*(i-m+1)/2+(n-i)*(n-i+1)/2);
for(re int i=m+1;i<=n;++i){
a.add(m-x[i-m],1),b.add(m-x[i-m],x[i-m]);
ans+=b.query(y[i])+(y[i]-m+1)*a.query(y[i]);
if(y[i]==m) ans-=a.query(y[i]);
ans-=a.query(0);
}
cout<<ans;
return 0;
}
|
数据范围开这么小随便做吧。
直接爆搜选哪些串,然后把长度为 的子串的哈希值存起来。
这样对于每一个哈希值可以求出它在每个串中各出现了多少次,乘起来即可。
复杂度
马拉车过于困难,考虑用哈希搞搞部分分。
部分分还是很好做的,我们处理出正着的哈希值和倒着的哈希值,然后枚举对称轴并二分长度,就做完了。
复杂度
事实上哈希也是能做到线性的,详见OI Wiki。
二分+哈希。
基本和上题一样。
处理出原串的哈希值和取反后的哈希值,然后枚举对称轴并二分长度。
对于统计答案,可以发现只有总长为偶数才可能合法。
然后没了。
简单题。
枚举左端点,然后二分长度,然后哈希判断有没有重复。
二分正确性也比较显然:如果当前长度不合法,那就必须变长,否则可以变短。
复杂度
感觉做不到 ,因为不管用 set,map 还是离散化都得带 ,所以题解复杂度是不是都写错了?
枚举哪个是插入的,然后把它删掉。
然后看剩下的东西能不能组成两个相同串即可。
这里还是稍微有点细节的,因为涉及到子串哈希值和把两个串拼接起来。
观察样例一,你会发现把枚举的那个删掉以后,因为要组成两个相同串,所以要保证两段长度相等。
所以要给短的那一段拼上一部分。
大概就是这样吧,其他应该没什么细节。
复杂度
如果 确定了,那么 也是确定的。
所以考虑枚举 和 ,这样做的好处是 是 级别的,所以总复杂度是 。
然后要解决的问题就是出现次数了。
我们可以维护出现次数为奇数次的个数的前缀和以及后缀和,那么查询用树状数组搞一下即可。
设 为字符集大小,复杂度 。
似乎需要卡常。
upd:完全不用卡。
而且没卡自然溢出,跑的飞快。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
| #include"bits/stdc++.h"
#define re register
#define int long long
#define ull unsigned long long
using namespace std;
const int maxn=2e6+10,maxm=30,V=26,base=131;
int n;
ull pw[maxn],h[maxn];
int buc[maxm];
int pre[maxn],suf[maxn];
char s[maxn];
struct BIT{
#define lb(x) (x&(-x))
int tr[maxm];
inline void add(int x,int val){++x;while(x<=V+1) tr[x]+=val,x+=lb(x);}
inline int query(int x){++x;int res=0;while(x) res+=tr[x],x-=lb(x);return res;}
inline void clear(){memset(tr,0,sizeof tr);}
#undef lb(x)
}a;
inline void init(){pw[0]=1;for(re int i=1;i<maxn;++i) pw[i]=pw[i-1]*base;}
inline int calc(int l,int r){return h[r]-h[l-1]*pw[r-l+1];}
inline void solve(){
cin>>(s+1);n=strlen(s+1);
for(re int i=1;i<=n;++i) h[i]=h[i-1]*base+s[i];
memset(buc,0,sizeof buc);
for(re int i=1;i<=n;++i){
++buc[s[i]-'a'];
if(buc[s[i]-'a']&1) pre[i]=pre[i-1]+1;
else pre[i]=pre[i-1]-1;
}
memset(buc,0,sizeof buc);
suf[n+1]=0;
for(re int i=n;i>=1;--i){
++buc[s[i]-'a'];
if(buc[s[i]-'a']&1) suf[i]=suf[i+1]+1;
else suf[i]=suf[i+1]-1;
}
int ans=0;a.clear();
for(re int len=1;len<=n;++len){
ull hs=calc(1,len);
for(re int r=len;r<n;r+=len){
int l=r-len+1;
if(calc(l,r)==hs) ans+=a.query(suf[r+1]);
else break;
}
a.add(pre[len],1);
}
cout<<ans<<'\n';
}
signed main(){
#ifndef ONLINE_JUDGE
freopen("1.in","r",stdin);
freopen("1.out","w",stdout);
#endif
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
init();int T;cin>>T;while(T--) solve();
return 0;
}
|
