笛卡尔树是一种二叉树，它既满足二叉搜索树的性质，又满足堆的性质。

例如 treap，就属于笛卡尔树的一种。

以下规定：第一键值为满足二叉搜索树的键值，第二键值为满足堆的键值。

构建

我们可以用单调栈做到 $O(n)$ 建树。

以对一个序列建树为例：我们将下标作为第一键值，权值作为第二键值。

那么每次我们插入的元素必然在这棵树的右链（右链：即从根节点一直往右子树走，经过的节点形成的链）的末端。

所以我们可以用单调栈来维护笛卡尔树的右链。

假设我们要建一颗大根笛卡尔树。

设当前位置为 $i$，前 $i-1$ 个位置已经构建好了。设栈顶元素为 $a_{top}$。

我们维护值单调递增的单调栈。

若 $a_i \le a_{top}$，直接将 $i$ 入栈（也就是把 $i$ 挂在右链上）。

否则一直弹栈，直到栈空或 $a_i \le a_{top}$。把最后一个弹出的元素设为 $i$ 的左儿子。

for(re int i=1;i<=n;++i){
    int tmp=top;
    while(tmp&&a[stk[tmp]]<a[i]) --tmp;
    if(tmp) rs[stk[tmp]]=i;
    if(tmp<top) ls[i]=stk[tmp+1];
    stk[++tmp]=i;
    top=tmp;
}

事实上，如果要按某个值作为第一键值，那么按这个值排序即可。

可以发现，笛卡尔树的根就是 stk[1]。

应用

笛卡尔树大多用来 dp。

对原问题转化后，变为笛卡尔树上的 dp 问题。

而且一般只会用到思想，并不会真把树建出来。

以及一些直方图似乎也会用到。

对于直方图类问题，我们常把下标作为第一键值，$h_i$ 作为第二键值建立小根笛卡尔树。

例题

[TJOI2011] 树的序

一道考察笛卡尔树定义的题。

题目给的很明白了，要按权值当第一键值。

因为要求字典序最小的生成序列，所以我们把每个数在序列中的位置当作第二键值，然后建小根笛卡尔树即可。

因为插入顺序是父亲->左儿子->右儿子，所以输出先序遍历即可。

注意输出的是键而不是编号。

Largest Rectangle in a Histogram

笛卡尔树求矩形面积板子题。

我们把下标作为第一键值，$h_i$ 作为第二键值建立小根笛卡尔树。

枚举点 $u$，看当 $h_u$ 作为矩形的高度时的最大面积。

因为我们建的是小根树，所以子树内的点的 $h_i$ 都大于 $h_u$。

因为下标是键，所以子树内的点构成一段连续区间。

那么以 $h_u$ 作为高时的最大面积为 $siz_u\times h_u$。

事实上有简单单调栈做法。

[COCI2008-2009#4] PERIODNI

我们考虑把这个多边形转成树。

受上题启发，我们把下标作为第一键值，$h_i$ 作为第二键值建立小根笛卡尔树。

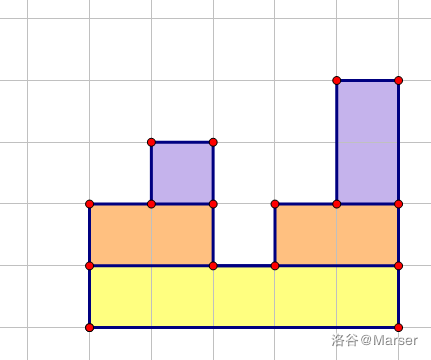
我们每次找到最低点，分成左右两边，然后递归处理。

不难发现，这些矩形对应笛卡尔树上的所有节点。

对于点 $u$,它代表的长为 $siz_u$，宽为 $h_u-h_{fa}$。

因为两个儿子是分开的，所以可以直接合并，没有影响。

设 $f_{u,i}$ 表示以 $u$ 为根的子树放了 $i$ 个的方案数，$g_{u,i}$ 表示以 $u$ 为根的子树放了 $i$ 个，且不包括 $u$ 代表的矩形的方案数。

那么 $g$ 的转移就是背包。

$$g_{u,i}=\sum_{j=0}^i f_{ls,j}\times f_{rs,i-j}$$

至于 $f$ 的转移，就是考虑 $u$ 放几个。

有结论：大小为 $n\times m$ 的棋盘，放 $k$ 个互不攻击的车，方案数为 $\binom{n}{k}\times \binom{m}{k}\times k!$

那么枚举子树一共用了几个，剩下的就是自己用的。

注意子树用了的自己不能用。

$$f_{u,i}=\sum_{j=0}^i \binom{siz_u}{i-j}\times \binom{h_u-h_{fa}}{i-j}\times (i-j)!\times g_{u,j}$$

复杂度 $O(nk^2+n^2)$

Yet Another Array Counting Problem

以下标为第一键值，$a_i$ 为第二键值建立大根笛卡尔树，那么 $[l,r]$ 的最左端最大值位置就是 $l,r$ 在笛卡尔树上的 $\operatorname{lca}$。

那么所有最左端最大值位置都相等，就意味着笛卡尔树的形态相同。

此时转化为树计数问题。

设 $f_{u,i}$ 表示 $u$ 取值 $1 \sim i$ 的方案数。

左儿子可以填 $[1,i-1]$，右儿子可以填 $[1,i]$

转移就是 $f_{u,i}=f_{u,i-1}+f_{ls_u,i-1}\times f_{rs_u,i}$

复杂度 $O(nm)$