学一遍不会一遍，遂决定写篇博客把东西记下来。

主要还是记录怎么做题。

定义与性质

这一部分还是详见OI Wiki吧。

常见方法

定义法

对于一些题目来说，我们只需要根据期望的定义 $E(X)=\sum p_ix_i$，把期望转化为求概率，再把概率转化为数数，然后再想办法怎么计数即可。

还有一种方法就是用 $\frac {所有情况的总价值}{总情况数}$ 来得到期望。

因为这种题目的难点都不在期望，只是套了个期望的壳子而已，所以我一般把这种题称作“假期望题”。

这种题目还挺多，例如最近做的几道：

纯粹的弹幕地狱：难点在后面的计数+莫反

不可思议的迷宫：难点在后面的分讨

符卡对决：难点在后面的莫队

不过也是有一些期望题能用定义做的，不过用这个方法做起来会比较麻烦。

但毕竟是定义，所以我一做题就会先想到这个···

期望的线性性

期望的线性性是一个非常好的性质：它让我们能够把贡献拆开分别统计，最后再合起来得到答案。

拆贡献也是一种非常常见且重要的思想。

DP

虽然说是 DP，但也有很多种状态设计。

例如：正推，逆推等。

在有关概率与期望的 DP 中，可以把每个状态看成一个节点，然后把 DP 的转移看成图上走路，这样会很好理解（事实上很多 DP 都能这么考虑吧）。

例题

下面我用例题带大家感受上面的方法应该如何运用。

绿豆蛙的归宿

方法一：利用期望的线性性

因为要求路径期望总长度，所以可以把路径拆成边，那么就要求每条边产生的期望贡献之和。

一条边产生的贡献的期望，根据期望的定义，等于这条边被经过的概率乘上边权。

所以只需要求每条边被经过的概率即可。

这里有一个套路：算边被经过的概率转化为求点被经过的概率。

设 $f_u$ 表示点 $u$ 被经过的概率，$deg_u$ 表示点 $u$ 的出度，若存在有向边 $(u,v)$，则

$$f_v=\sum \frac {f_u}{deg_u}$$

那么边 $(u,v)$ 被经过的概率为 $\frac {f_u}{deg_u}$。

答案就是把每条边的贡献的期望值加起来。

#include"bits/stdc++.h"
#define re register
#define int long long 
#define double long double
using namespace std;
const int maxn=1e5+10,maxm=2e5+10;
int n,m,cnt;
int head[maxn],in[maxn],deg[maxn];
double ans,f[maxn];
struct edge{
    int to,nxt,w;
}e[maxm];
inline void add(int u,int v,int w){
    ++in[v],++deg[u];
    e[++cnt]={v,head[u],w};
    head[u]=cnt;
}
inline void topo(){
    queue<int> q;
    for(re int u=1;u<=n;++u) if(!in[u]) q.push(u);
    while(!q.empty()){
        int u=q.front();q.pop();
        for(re int i=head[u];i;i=e[i].nxt){
            int v=e[i].to;
            if(!(--in[v])) q.push(v);
            f[v]+=f[u]/deg[u];
            ans+=f[u]/deg[u]*e[i].w;
        }
    }
}
signed main(){
#ifndef ONLINE_JUDGE
    freopen("1.in","r",stdin);
    freopen("1.out","w",stdout);
#endif
    ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
    cin>>n>>m;
    for(re int i=1,u,v,w;i<=m;++i) cin>>u>>v>>w,add(u,v,w);
    f[1]=1;topo();
    printf("%.2Lf",ans);
    return 0;
}

方法二：DP

正推和逆推都是可以的，这里讲逆推。

设 $f_u$ 表示从 $u$ 到 $n$ 的路径期望总长度，若存在有向边 $(u,v)$，则转移为

$$f_u=\frac {1}{deg_u}\sum f_v+w_{u,v}$$

因为转移是 $v$ 向 $u$ 贡献，所以要建反图，然后在反图的拓扑序上 DP。

初值为 $f_n=0$，答案为 $f_1$。

注意：因为建了反图，所以转移里的 $u,v$ 也变了。请仔细理解。

#include"bits/stdc++.h"
#define re register
#define int long long 
#define double long double
using namespace std;
const int maxn=1e5+10,maxm=2e5+10;
int n,m,cnt;
int head[maxn],in[maxn],deg[maxn];
double f[maxn];
struct edge{
    int to,nxt,w;
}e[maxm];
inline void add(int u,int v,int w){
    ++in[v],++deg[v];
    e[++cnt]={v,head[u],w};
    head[u]=cnt;
}
inline void topo(){
    queue<int> q;
    for(re int u=1;u<=n;++u) if(!in[u]) q.push(u);
    while(!q.empty()){
        int u=q.front();q.pop();
        for(re int i=head[u];i;i=e[i].nxt){
            int v=e[i].to;
            if(!(--in[v])) q.push(v);
            f[v]+=1.0*(f[u]+e[i].w)/deg[v];
        }
    }
}
signed main(){
#ifndef ONLINE_JUDGE
    freopen("1.in","r",stdin);
    freopen("1.out","w",stdout);
#endif
    ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
    cin>>n>>m;
    for(re int i=1,u,v,w;i<=m;++i) cin>>u>>v>>w,add(v,u,w);
    topo();
    printf("%.2Lf",f[1]);
    return 0;
}

Beautiful Mirrors

利用这道题介绍期望 DP 的各种 trick。

以下的 $p_i$ 为题目中的 $\frac {p_i}{100}$。

方法一：正推

设 $f_i$ 表示从第一面镜子到第 $i$ 面镜子都高兴的期望天数。

那么在第 $i$ 天，有以下两种可能：

1. 询问失败，概率为 $1-p_i$。代价为 $f_{i-1}+1+f_i$。
2. 询问成功，概率为 $p_i$。代价为 $f_{i-1}$。

根据期望的定义，概率乘代价再求和就是期望。则

$$f_i=(1-p_i)(f_{i-1}+1+f_i)+p_i(f_{i-1}+1)$$

移项，整理得

$$f_i=p_i(f_{i-1}+1)$$

初值为 $f_0=0$，答案为 $f_n$。

可能有疑问：为什么询问失败的代价为 $f_{i-1}+1+f_i$？

可以把代价拆开来看。

首先，我们已经到了第 $i$ 面镜子，说明前 $i-1$ 面都没失败，这部分的代价为 $f_{i-1}$。

然后，我们在第 $i$ 面镜子处进行询问，会花费一天，这部分的代价为 $1$。

最后，因为询问失败，我们回到了第一面镜子。但我们的状态为从第一面镜子到第 $i$ 面镜子都高兴，所以我们还得从第一面镜子一直问到第 $i$ 面镜子且保持高兴。这部分的代价为 $f_i$。

方法二：逆推

设 $f_i$ 表示从第 $i$ 面镜子到最后一面镜子的期望天数。

那么在第 $i$ 天，有以下两种可能：

1. 询问失败，概率为 $1-p_i$，我们会回到第一面镜子，代价为 $f_1+1$。
2. 询问成功，概率为 $p_i$，我们会走到下一面镜子，代价为 $f_{i+1}+1$。

根据期望的定义，概率乘代价再求和就是期望。则

$$f_i=(1-p_i)(f_1+1)+p_i(f_{i+1}+1)$$

初值为 $f_{n+1}=0$，答案为 $f_1$。

要求 $f_1$，但是转移用到了 $f_1$，考虑解方程。

如果你把前几项写出来，会发现：

当 $i=1$ 时，$f_1=f_2+\frac {1}{p_1}$。

当 $i=2$ 时，$f_1=f_3+\frac {1+\frac {1}{p_1}}{p_2}$。

当 $i=3$ 时，$f_1=f_4+\frac {1+\frac {1+\frac {1}{p_1}}{p_2}}{p_3}$。

所以：

$$f_1=\frac {1+\frac {1+\frac {\cdots}{p_{n-2}}}{p_{n-1}}}{p_n}$$

整理得：

$$f_1=\frac {1+p_1+p_1p_2+\cdots+p_1p_2\cdots p_{n-1}}{\prod_{i=1}^np_i}$$

方法三：一种常见的状态设计但是我不知道怎么称呼

设 $f_i$ 表示从第 $i$ 面镜子到第 $i+1$ 面镜子的期望天数。

设 $s=\sum_{j=1}^{i-1} f_j$，则

$$f_i=p_i\times 1+(1-p_i)\times (1+f_i+s)$$

关于代价为什么是这个，可以参考正推。

移项，整理得：

$$f_i=\frac {1+(1-p_i)\times s}{p_i}$$

答案为 $\sum_{i=1}^n f_i$。

方法四：设一次函数

还是逆推的 DP。

设 $f_i=k_i\times f_1+b_i$，通过递推求出 $k_{n+1},b_{n+1}$，最后解方程 $k_{n+1}\times f_1+b_{n+1}=0$ 即可。

[六省联考 2017] 分手是祝愿

一道经典好题。

利用这道题补充期望 DP 的各种 trick。

首先考虑最优操作应该怎么按。

感性理解一下，可以发现：每次按最右边的是最优的。因为除它以外没有数的约数包含它，所以它必须得按。

事实上，这也是唯一的一种按法。证明参考题解。

考虑 DP。

设 $f_i$ 表示当前还剩 $i$ 个键要按的期望操作次数，则转移为：

$$f_i = \begin{cases} i & (i \le k) \\ \frac {i}{n} f_{i-1}+\frac {n-i}{n}f_{i+1}+1 & (i >k) \end{cases}$$

这应该挺好理解的吧，不再赘述了。

但是这东西没法转移啊，只能高斯消元解方程，怎么办？

方法一：模拟高斯消元

事实上，如果你把系数矩阵写出来，会发现它长这样（图片来自题解）：

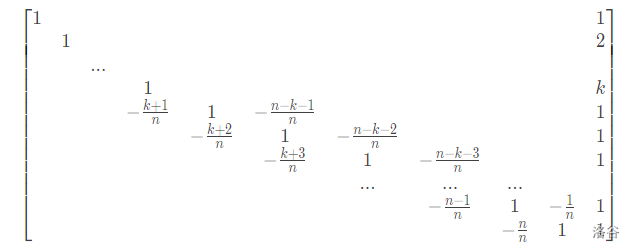
对于这种带状矩阵，有复杂度为 $O(nd^2)$ 的消元方法。

具体可以参考文章：浅谈高斯消元拓展之 band-matrix。

但高斯消元这东西我学一次忘一次···

方法二：设一次函数

设 $f_i=f_{i-1}+b_i$，那么发现 $b_i$ 是好求的。

转移为

$$f_i=\frac {i}{n} f_{i-1}+\frac {n-i}{n}f_{i+1}+1$$

代入得

$$f_i=\frac {i}{n} (f_i-b_i)+\frac {n-i}{n}(f_i+b_{i+1})+1$$

发现 $f_i$ 被消没了，则

$$b_i = \frac {(n-i)b_{i+1}+n}{i}$$

边界为 $b_n=1$。

然后用 $b_i$ 把 $f_i$ 求出来即可。

方法三：一种常见的状态设计

把之前的 DP 扔了，换状态。

设 $f_i$ 表示从还剩 $i$ 个键要按到还剩 $i-1$ 个键要按的期望操作步数。

那么还剩 $i$ 个键时，有以下两种可能：

1. 按对了，概率为 $\frac {i}{n}$，代价为 $1$。
2. 按错了，概率为 $\frac {n-i}{n}$，代价为 $f_i+f_{i+1}+1$。

则转移为

$$f_i = \frac {i}{n}+ \frac {n-i}{n}\times(f_i+f_{i+1}+1)$$

为什么代价是这个？

感觉和之前那个一样吧，但还是再解释一遍：

可以把代价拆开来看。

首先，我们按了一次，代价为 $1$。

然后，因为按错了，所以现在还剩 $i+1$ 个键需要按。那么从还剩 $i+1$ 个键到还剩 $i$ 个键的代价为 $f_{i+1}$。

最后，我们需要把还剩 $i$ 个键变成还剩 $i-1$ 个键（因为这是我们的状态），代价为 $f_i$。

我们先按最优解的操作按一遍，得到操作次数 $cnt$。那么答案为

$$\begin{cases}cnt & (cnt \le k) \\ (\sum_{i=k+1}^{cnt} f_i)+k & (cnt > k)\end{cases}$$

[SHOI2002] 百事世界杯之旅

设 $f_i$ 表示当前已经拿了 $i$ 种物品，那么转移为

$$f_i=\frac {i}{n}f_i+\frac {n-i}{n}f_{i+1}+1$$

移项整理得

$$f_i=f_{i+1}+\frac {n}{n-i}$$

初值为 $f_n=0$，答案为 $f_0$。

事实上，你把式子再写一下，会发现 $f_0=\sum_{i=1}^n \frac {n}{i}$。

Let’s Play Osu!

加强版：OSU!

设 $f_i$ 表示以 $i$ 结尾连续成功长度的期望，$g_i$ 表示以 $i$ 结尾连续成功长度的平方的期望。

然后根据期望的线性性，$E((X+1)^2)=E(X^2+2X+1)=E(X^2)+2E(X)+1$。

所以转移为

$$f_i=p_i\times (f_{i-1}+1) \\ g_i=p_i\times (g_{i-1}+2\times f_{i-1}+1)$$

弱化版答案为 $\sum_{i=1}^n p_i\times (2\times f_{i-1}+1)$。

加强版答案为 $\sum_{i=1}^n p_i\times (3\times g_{i-1}+3\times f_{i-1}+1)$。

[Cnoi2020] 线形生物

期望的线性性好题。

设 $f_{u \rightarrow v}$ 表示 $u$ 到 $v$ 的期望步数，则 $f_{u \rightarrow v}=\sum_{i=u}^{v-1} f_{i \rightarrow i+1}$。

设 $g_u$ 表示 $u$ 到 $u+1$ 的期望步数，$deg_u$ 表示 $u$ 的返祖边条数，$E$ 为 $u$ 的返祖边集，则

$$g_u=\frac {1}{deg_u+1}\times 1+\frac {1}{deg_u+1}\times\sum_{(u,v)\in E} (f_{v,u+1}+1)$$

设 $s_i=\sum_{j=1}^i g_i$，则

$$g_u=1+\frac {1}{deg_u+1}\times\sum_{(u,v)\in E}s_u-s_{v-1}$$

把 $g_u$ 都放到左边，整理得

$$g_u=(deg_u+1)+\sum_{(u,v)\in E}s_{u-1}-s_{v-1}$$

答案为 $s_n$。

[HNOI2013] 游走

高斯消元经典题。

设 $f_u$ 表示点 $u$ 得期望经过次数，$g_{u,v}$ 表示边 $(u,v)$ 的期望经过次数，$deg_u$ 表示点 $u$ 的出度，则

$$g_{u,v}=\frac {f_u}{deg_u}+\frac {f_v}{deg_v} \\ f_u=\sum \frac {f_v}{deg_v}$$

然后高斯消元把 $f$ 求出来，再用 $f$ 把 $g$ 求出来即可。

至于编号，我们只需要贪心的给期望经过次数越大的边编号越小即可。

忽略了很多细节，写的时候需要注意。

Broken robot

也是高斯消元经典题。

设 $f_{i,j}$ 表示从 $(i,j)$ 走到最后一行的期望步数，转移为

$$f_{i,j}= \begin{cases} \frac{f_{i+1,j}+f_{i,1}+f_{i,2}}{3}+1 & (j=1) \\ \frac{f_{i+1,m}+f_{i,m}+f_{i,m-1}}{3}+1 & (j=m) \\ \frac{f_{i+1,j}+f_{i,j}+f_{i,j+1}+f_{i,j-1}}{4}+1 & otherwise \end{cases}$$

初始值为 $f_{n,i}=0$。

因为只能往下走，所以行没有后效性，但列有后效性。

所以从下往上消元即可。

暴力消元复杂度不对，但是你把系数矩阵写出来，发现又是带状矩阵。

所以按之前的方法消元就行了。

[HNOI2015] 亚瑟王

根据期望的线性性，总伤害就是每张卡的伤害乘上该卡的发动概率，所以考虑如何求出每张卡的发动概率。

这道题最难的地方就是轮次，如果根据轮次来 DP 的话，会发现有后效性。例如我一开始想的是 $f_{i,j}$ 表示第 $i$ 轮发动 $j$ 的概率，发现转移不了。

我们换一个思路，既然轮次有后效性，那就不能按轮次 DP 了，而是直接考虑卡牌。

感觉是和荷取融合很像的套路。

设 $f_{i,j}$ 表示在整局游戏中，前 $i$ 张牌发动了 $j$ 张的概率，则转移为

$$f_{i,j}=f_{i-1,j}\times (1-p_i)^{r-j}+f_{i-1,j-1}\times (1-(1-p_i)^{r-j+1})$$

解释一下这个转移。

如果 $f_{i,j}$ 从 $f_{i-1,j}$ 转移来，说明第 $i$ 张牌在整局游戏中都没有发动。

因为前面已经发动了 $j$ 张，也就是占用了 $j$ 轮的机会，所以概率为 $(1-p_i)^{r-j}$。

如果 $f_{i,j}$ 从 $f_{i-1,j-1}$ 转移来，说明第 $i$ 张牌发动了。

但发动的概率不好求，考虑用 $1$ 减去不发动的概率，为 $(1-p_i)^{r-j+1}$。

那每张卡的发动概率就好求了：

$$P_i=\sum \limits_{j=0}^{i-1} f_{i-1,j}\times (1-(1-p_i)^{r-j})$$

[NOIP2016 提高组] 换教室

感觉比较简单。

设 $f_{i,j,0/1}$ 表示前 $i$ 节课成功换了 $j$ 次教室。

转移就是考虑换不换，如果换还要考虑能否成功，乘上最短路长度即可。

是没啥意思的分类讨论，不展开写了。

最短路用 Floyd 预处理即可。